Josh Berryman Science Page
This is a page that I maintain myself to publicise my work and share code for download. I also have an entry in the online staff directory at the University of Luxembourg. Previously I have worked as an assistant to Prof. Tanja Schilling here in Luxembourg; also I have postdoc'd in the KOMET 331 group in Mainz. I did my PhD in Leeds, co-supervised by Sarah Harris and Sheena Radford; and my other degrees at Edinburgh.
My research is mostly in the region of computational molecular biology, chemical physics and physical chemistry. Right now most of my effort is spent developing novel simulation and search techniques. I publish mostly in journals that have "phys" "chem" "bio" or "comput" in their names.
Some Example Research Topics
DNA Mechanics
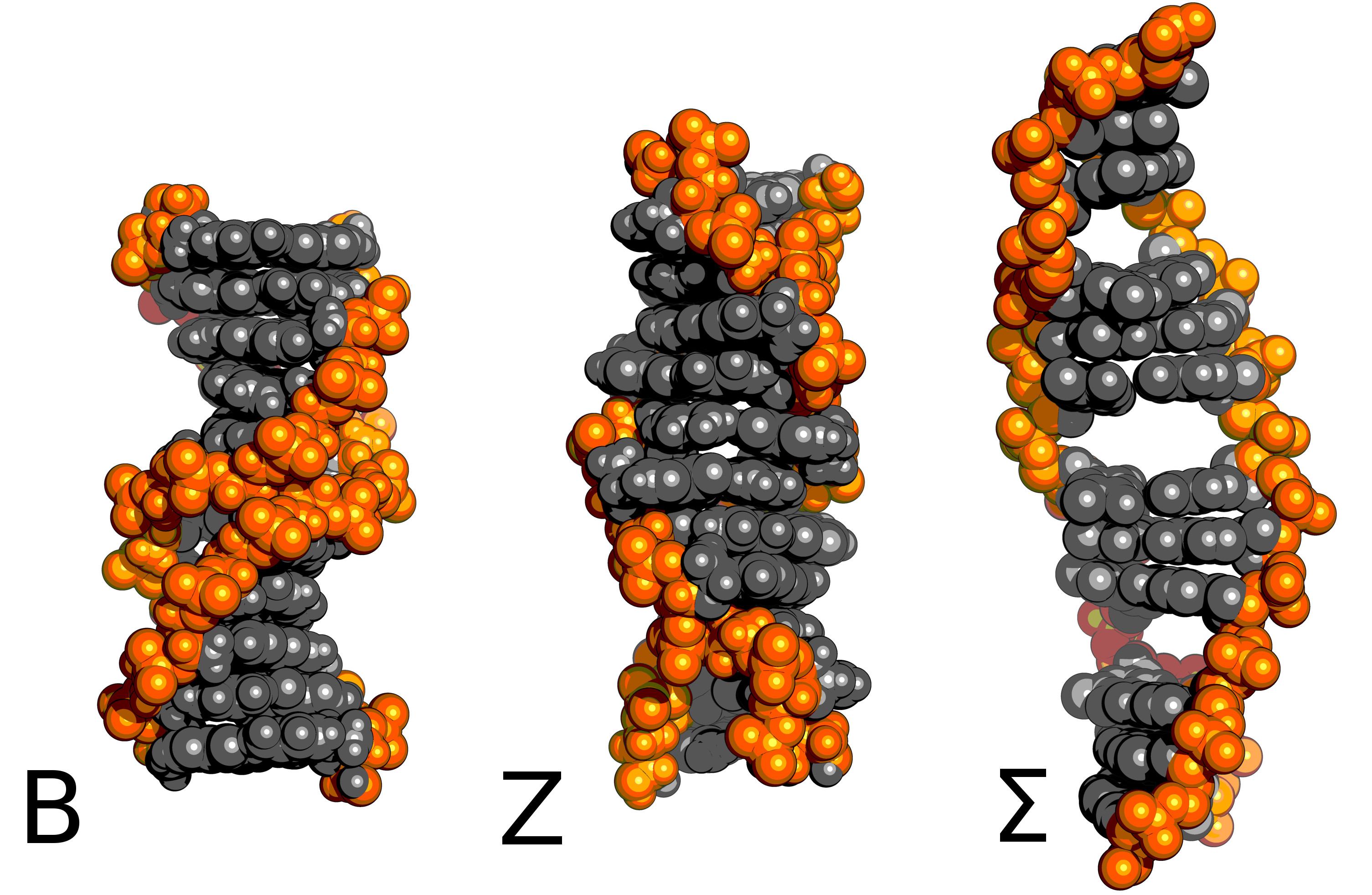 What happens when you pull on one end of a DNA double-helix? The answer, surprisingly, is still not entirely clear. What happens would appear to depend on the sequence, the solution conditions and the precise way that you pull (fast/slow/exact atom to apply the force on...).
What happens when you pull on one end of a DNA double-helix? The answer, surprisingly, is still not entirely clear. What happens would appear to depend on the sequence, the solution conditions and the precise way that you pull (fast/slow/exact atom to apply the force on...).
B-phase DNA is the familar right-handed double-helix. In near-saturated salt solution or with left-handed twisting you can expect Z-DNA. With tension, the right sequence, and the right co-factors in solution you might get Σ-DNA.
Free Energy Calculation
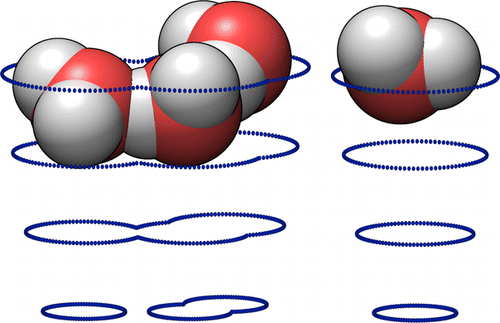 The difference in Free Energy between two systems is an indicator of the balance of their chemical equilibrium. It is difficult to calculate the free energy for complex systems, especially those including some interaction with solvent, due to the large number of distinct microstates which typically correspond to an observable macrostate.
The difference in Free Energy between two systems is an indicator of the balance of their chemical equilibrium. It is difficult to calculate the free energy for complex systems, especially those including some interaction with solvent, due to the large number of distinct microstates which typically correspond to an observable macrostate.
The small image on the right shows a handful of water molecules moving on the potential surface which is generated for them by the large number of other water molecules not shown.
I have written a tutorial on one (of the many) methods of free energy calculation, giving step by step instructions to achieve results using the EMIL module which I wrote for AMBER. EMIL works either with the open source simulation kernel of AMBER [get SANDER here] or with the paid-for simulation kernel [get PMEMD here], which is faster in most cases. The EMIL code is suitable for finding absolute free energies of biomolecules, in explicit or implicit solvent.
Time-Dependent Rare Event Dynamics
 I am interested in rare event calculations, particularly in time-evolving systems. The classic example is nucleation in a system with a time-dependent external driving force, such as an imposed shear flow.
I am interested in rare event calculations, particularly in time-evolving systems. The classic example is nucleation in a system with a time-dependent external driving force, such as an imposed shear flow.
In a landscape search, the object is to characterise a system in terms of the states which it can occupy at equilibrium; with the idea that dynamics either at or away from equilibrium can then be characterised as paths through this landscape. In a rare event search, the object is to identify and characterise a subset of the available paths of a system, typically seeking out those which represent a dramatic change in the collective state. This path-based formalism makes more sense when considering dynamics off equilibrium, or when you have a clear idea of the type of event which is interesting.
I and Tanja have invented a method for calculating rare-event pathways off-equilibrium. You can read about it in context on the wikipedia page "Stochastic Process Rare Event Sampling". Links and more discussion are here. The image of fractally generated tree branches (thankyou wikimedia) is intended as a poetic illustration of the spreading paths which a stochastic system can take through time.
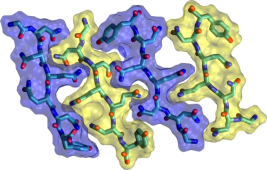
Protein Aggregation
Proteins can assemble to form linear filaments called amyloid fibrils. Molecular dynamics simulations of model amyloid fibrils can help us to understand how these toxic supramolecular aggregates form and spread. The image of interlocking peptide sidechains is taken from a set of molecular dynamics simulations which I carried out to explore some of the many configurations which are available for aggregates of even the smallest of peptides. You can read more about this on my publications page.
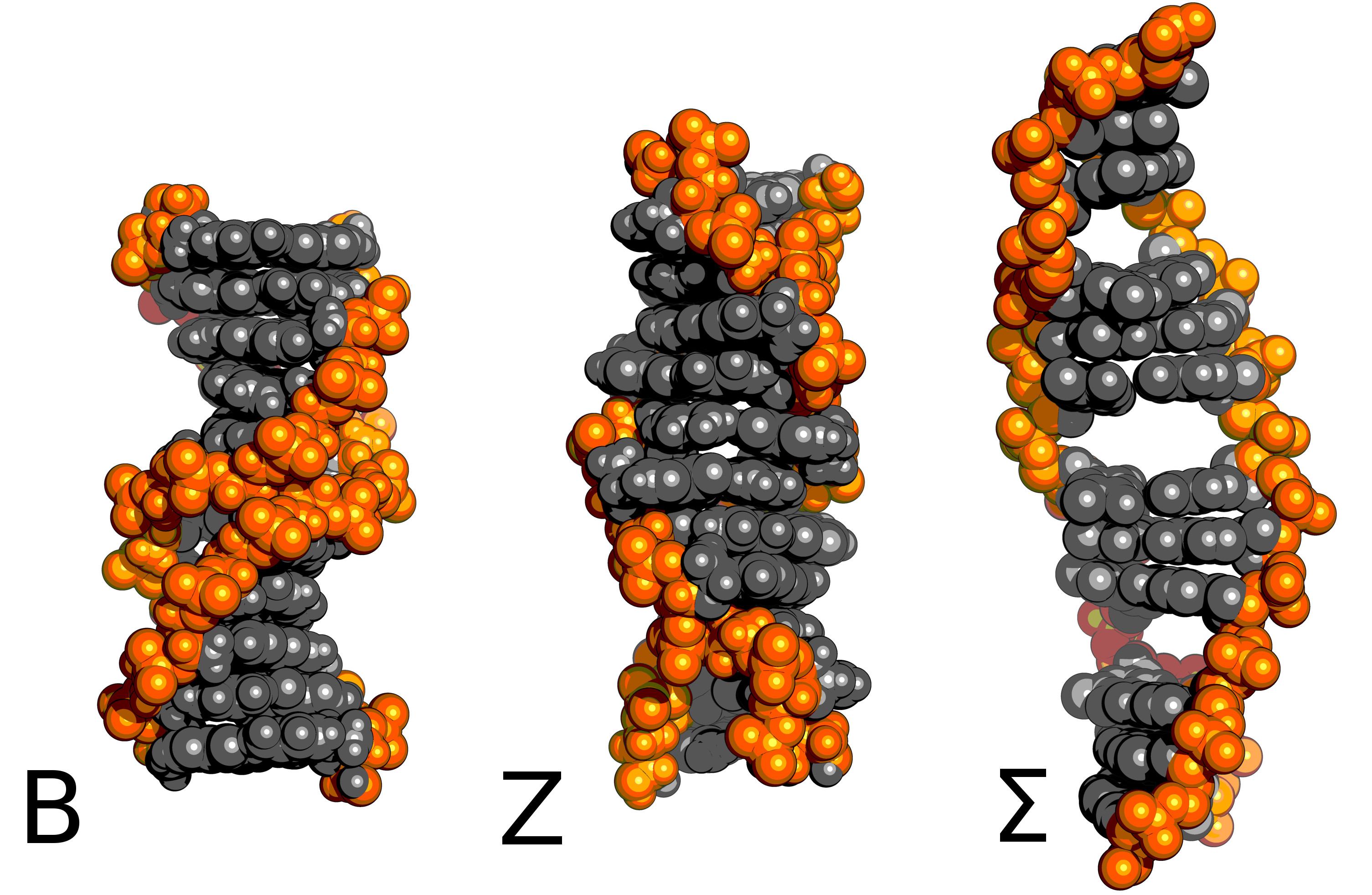 What happens when you pull on one end of a DNA double-helix? The answer, surprisingly, is still not entirely clear. What happens would appear to depend on the sequence, the solution conditions and the precise way that you pull (fast/slow/exact atom to apply the force on...).
What happens when you pull on one end of a DNA double-helix? The answer, surprisingly, is still not entirely clear. What happens would appear to depend on the sequence, the solution conditions and the precise way that you pull (fast/slow/exact atom to apply the force on...).
 The difference in Free Energy between two systems is an indicator of the balance of their chemical equilibrium. It is difficult to calculate the free energy for complex systems, especially those including some interaction with solvent, due to the large number of distinct microstates which typically correspond to an observable macrostate.
The difference in Free Energy between two systems is an indicator of the balance of their chemical equilibrium. It is difficult to calculate the free energy for complex systems, especially those including some interaction with solvent, due to the large number of distinct microstates which typically correspond to an observable macrostate.
 I am interested in rare event calculations, particularly in time-evolving systems. The classic example is nucleation in a system with a time-dependent external driving force, such as an imposed shear flow.
I am interested in rare event calculations, particularly in time-evolving systems. The classic example is nucleation in a system with a time-dependent external driving force, such as an imposed shear flow.
